במאמר הקודם שלי הצגתי את מרכזיותו של המספר שבע בהגותם של האיסיים. האיסיים ייחסו חשיבות רבה לחלוקת הזמן למרכיבים שביעוניים: שבוע, שבת, שמיטה (שבע שנים) ויובל (שבע שמיטות שהן 49 שנים). כמו כן הם אימצו את לוח השמש השביעוני, שמבוסס על 364 ימים שהם 52 שבועות.
המרכזיות של המספר שבע אצל האיסיים לא הייתה מוגבלת רק לאופן ספירת הזמן, אלא היה לה גם ביטוי קוסמי ורוחני. הדומיננטיות של המספר שבע נחשבה כביטוי לחוק אלוהי שמשתקף הן בעולם הנגלה והן בעולמות הרוחניים. המספר שבע, והביטוי שלו בלוח השמש השביעוני של האיסיים, משקפים חוק קוסמי שמקורו בהתגלות אלוהית ולא במוסכמה אנושית.
ניסוח חדש יותר של "חוק השבע" נמצא בכתביו של גיאורג איבאנוביץ' גורדייף, מורה רוחני ממוצא יווני־ארמני (1949-1870). גורדייף הציג דרך רוחנית ייחודית שאותה הוא כינה "הדרך הרביעית", שנלמדת עד היום במסגרות שונות. גורדייף ערך מסעות רבים ברחבי אסיה והמזרח התיכון, בחיפוש אחר ידע שנשתמר בתוך תרבויות ומסורות עתיקות. הוא ביקר ושהה במנזרים ובבתי ספר ממסורות שונות וחקר את התורות הרוחניות שנלמדו שם. בין היתר הוא מספר בכתביו שהוא שהה ולמד במנזרים איסיים.
משנתו של גורדייף מתמקדת בחוקיות ששוררת ביקום, הן במימד הפיזי והן במימד הרוחני. גורדייף טען שאותם חוקים פועלים בכל הממדים של היקום, ולכן על האדם ששואף להתפתחות רוחנית ללמוד את החוקים האלה ולהשתמש בהם לצורך התפתחותו. גורדייף ניסח בצורה מפורשת את "חוק השבע", שהוא קרא לו "חוק האוקטבה", כחוק שמתאר כיצד פועלים תהליכי התפתחות בעולם, הן במישור הפיזי והן במישור הרוחני. התהליך מתואר כעליה בתדירותן של התנודות, כאשר בין הרמה ההתחלתית לרמה שבה התדירות מוכפלת ישנן שבע דרגות. תהליך ההתפתחות האנושי איננו שונה מכל תהליך אחר של עליה מרמה אחת לרמה גבוהה יותר (או עליה בתדירות התנודות בטרמינולוגיה של גורדייף), ולכן גם הוא כפוף לחוק השבע.
במאמר זה ברצוני להרחיב את הדיון בחוק האוקטבה ולהראות את הקשר שלו גם לעולם הפיזי. אם אכן חוק האוקטבה עומד בבסיס של כל תהליכי ההתפתחות, היינו מצפים לראות אותו גם בתהליכי התפתחות שקיימים בטבע. בהמשך אציג ממצאים שממחישים כיצד תהליכי ההתפתחות בטבע מבוססים על מחזוריות דומה לזאת שאנו רואים באוקטבה המוסיקלית, שמבטאת את חוק השבע. ממצאים אלה קיימים הן ברמה המולקולרית של החומר והן בתהליכי התפתחות של צמחים ובעלי חיים.
חוק האוקטבה
גורדייף השתמש באוקטבה המוסיקלית כמודל להצגתו של חוק השבע. מבנה האוקטבה המוסיקלית מוצג בטבלה שלהלן.
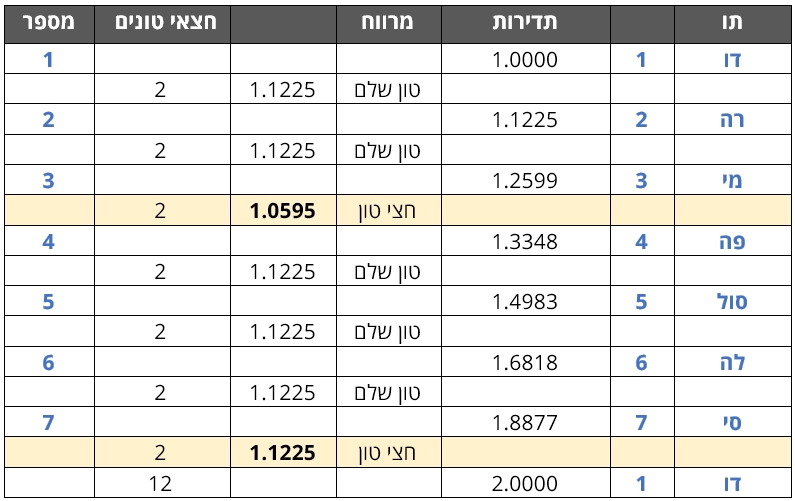
בין התו דו באוקטבה אחת לתו דו באוקטבה שמעליה מוכפלת תדירותו של הצליל. המרווחים בתוך האוקטבה מחולקים ל-7 תווים ול-12 חצאי טונים. העלייה בתדר הצליל בין כל חצי טון היא בשיעור של 1.0594631, והיא מתקבלת באמצעות הקשר:
2 = 1.059463112
החלוקה הלא־סימטרית של התווים והטונים (7 תווים שמכילים 12 חצאי טונים) מצביעה על כך שהמרווחים בין התווים אינם שווים: בין התווים דו-רה, רה-מי, פה-סול, סול-לה, לה-סי ישנו מרווח של שני חצאי טונים (טון שלם).
כלומר העלייה בתדר הצליל בין התווים האלה היא בשיעור של 1.1224621 שמתקבל באמצעות הקשר:
1.1224621 = 1.05946312
לעומת זאת בין התווים מי-פה וסי-דו ישנם מרווחים של חצי טון, כלומר העלייה בתדר הצליל היא בשיעור של 1.0594631.
במילים אחרות, המרווחים בין התווים שמשקפים את העלייה בתדר הצליל עד להכפלתו, אינם רציפים. ישנן 5 מרווחים של שני חצאי טונים ו-2 מרווחים של חצי טון בלבד. נקודות אי הרציפות הן במעבר משלב 3 (התו מי) לשלב 4 (התו פה), ובמעבר משלב 7 (התו סי) לשלב 8, שהוא שלב 1 של האוקטבה הבאה (התו דו).
במאמר הקודם הראיתי שחוק האוקטבה, היה המוטיב המרכזי בכתבי האיסיים, שעוסקים בהרחבה בחשיבותו של המספר שבע. העדות של גורדייף לגבי הקשר הישיר שלו עם מסדרים איסיים, תומכת בהשערה שהוא קבל את הידע הזה מהם.
חוק האוקטבה ויחס הזהב
ביטוי נוסף לחוק האוקטבה ניתן למצוא בגודל מתמטי שנקרא "יחס הזהב". יחס הזהב הוא מספר אי־רציונלי ששווה בקירוב ל-1.618. את יחס הזהב ניתן לגזור מסדרה מתמטית שנקראת סדרת פיבונצ'י. והיא מוצגת בטבלה שלהלן.

בסדרת פיבונצ'י כל איבר הוא הסכום של שני המספרים שלפניו (למעט שני האיברים הראשונים 0 ו-1). בניית הסדרה היא פשוטה מאוד: האיבר השלישי הוא 1 (הסכום של 1+0), האיבר הרביעי הוא 2 (הסכום של 1+1), האיבר החמישי הוא 3 (הסכום של 2+1) וכך הלאה.
אחת התכונות של סדרת פיבונצ'י היא שהיחס בין כל שני איברים עוקבים מתכנס ליחס הזהב. כך למשל היחס בין 34 ל-21 הוא 1.619, היחס בין 55 ל- 34 הוא 1.6176 והיחס בין 89 ל-55 הוא 1.6182. ככל שאיברי הסדרה גדלים היחס בין שני איברים עוקבים מתקרב ליחס הזהב.
את יחס הזהב אנו יכולים לראות בטבע אם נציג את סדרת פיבונצ'י באמצעות ריבועים שאורך הצלע שלהם שווה לערך הסדרה, כדוגמת לכך התרשים שלהלן.
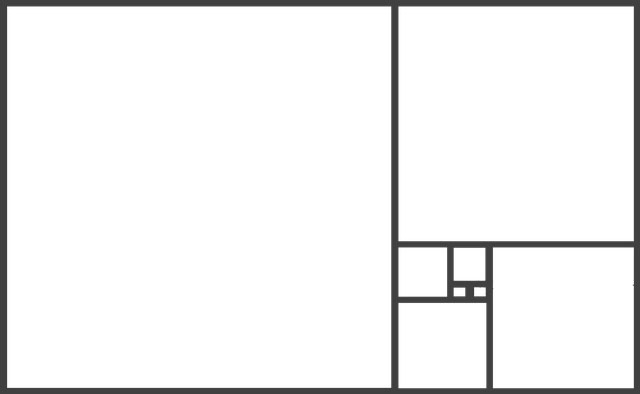
חיבור הריבועים יוצר מלבן שהיחס בין צלעותיו הוא היחס בין האיברים שבסדרת פיבונצ'י. לפיכך ככל שנגדיל את מספר הריבועים היחס בין צלעות של המלבן שייווצר יתכנס ליחס הזהב. בתרשים שלעיל אורך הבסיס של המלבן הוא 34 ואורך הגובה שלו הוא 21. לפיכך היחס ביניהם הוא 1.619.
באמצעות התרשים שלעיל ניתן ליצור תבנית של ספירלה שמוצגת בתרשים שלהלן.

הספירלה נוצרת באמצעות תנועה לאורך אלכסוני הריבועים. בדוגמה שלהלן אנו משתמשים בקווים ישרים אולם ניתן ליצור את הספירלה גם אם נשרטט קשת במקום כל אלכסון, כפי שמוצג בתרשים שלהלן.
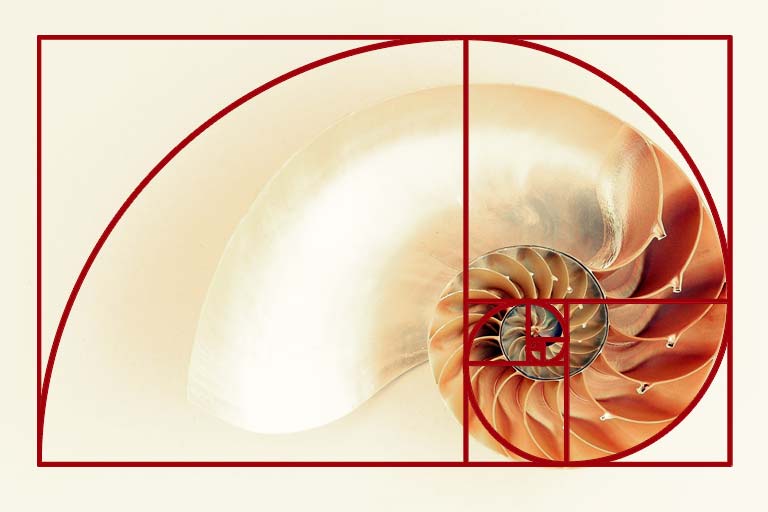
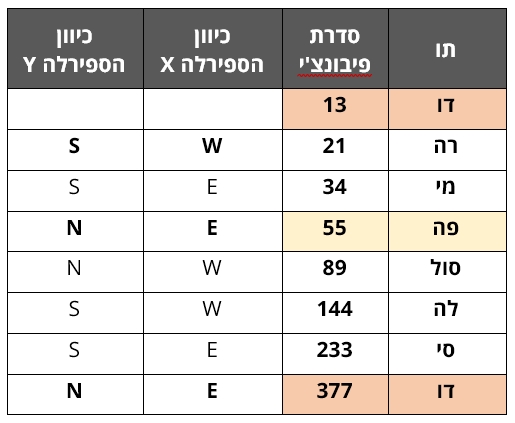
מסתבר שבאמצעות סדרת פיבונצ'י ניתן להגיע בדרך מתמטית לספירלה שהיא צורה שנפוצה מאוד בטבע כפי שנראה בהמשך. אולם לפני כן עלינו עדיין להראות כיצד בא לידי ביטוי חוק האוקטבה בסדרת פיבונצ'י. לשם כך נשתמש בתרשים הקודם שבו הספירלה נוצרה על ידי קווים ישרים שמייצגים את אלכסוני הריבועים. כל קו כזה מסומן בחץ שחור שמצביע על כיוון ההתפתחות של הספירלה – מבפנים החוצה. ליד כל חץ מופיעים בתרשים ערכי האיברים המתאימים של סדרת פיבונצ'י, וכן סדר הערכים על פי האוקטבה. כך למשל האיבר הראשון בסדרה הוא 0 והוא יופיע בבסיס החץ הראשון, כשהוא מקביל לתו הראשון דו. האיבר השני – 1 יופיע בבסיס החץ השני והוא מקביל לתו השני רה. נתוני התרשים מוצגים גם בטבלה שלהלן.

הטור השמאלי של הטבלה מציג את כיוון החץ שהוא למעשה כיוונה של הספירלה. בדוגמה שלנו כיוונו של החץ הראשון הוא לדרום־מזרח והוא מחבר בין התו דו לרה (או בין איבר 0 לאיבר 1). ניתן לראות שהחץ משנה את כיוונו בכל מעבר בין שני איברים, וכך למעשה נוצרת צורת הספירלה. ישנם שני מעברים שבהם כיוון החץ הוא בדיוק הפוך מהכיוון ההתחלתי – כלומר הוא פונה לצפון־מערב. המעבר הראשון הוא בין התו מי לפה (או בין האיבר 1 לאיבר 2) והמעבר השני הוא בין התו סי לתו דו (או בין איבר 8 לאיבר 13). אנו רואים אפוא שהספירלה שנוצרת על ידי סדרת פיבונצ'י (יחס הזהב) מתנהגת לפי חוק האוקטבה. שני המעברים שבהם הספירלה מחליפה כיוון מקבילים למעברים הלא רציפים בין התווים מי לפה וסי לדו.
הקשר בין ספירלת פיבונצ'י לחוק האוקטבה איננו תלוי בכיוון ההתחלתי של הספירלה, ומתקיים למעשה לכל אורכה. על מנת להראות זאת נציג להלן ספירלה שמשתרעת על פני שתי אוקטבות (כלומר על פני 15 האיברים הראשונים של סדרת פיבונצ'י). על מנת לעשות זאת יש צורך לתרגם את ספירלת פיבונצ'י לערכי X ו-Y במערכת צירים רגילה. שיטת התרגום מוצגת בטבלה שלהלן.
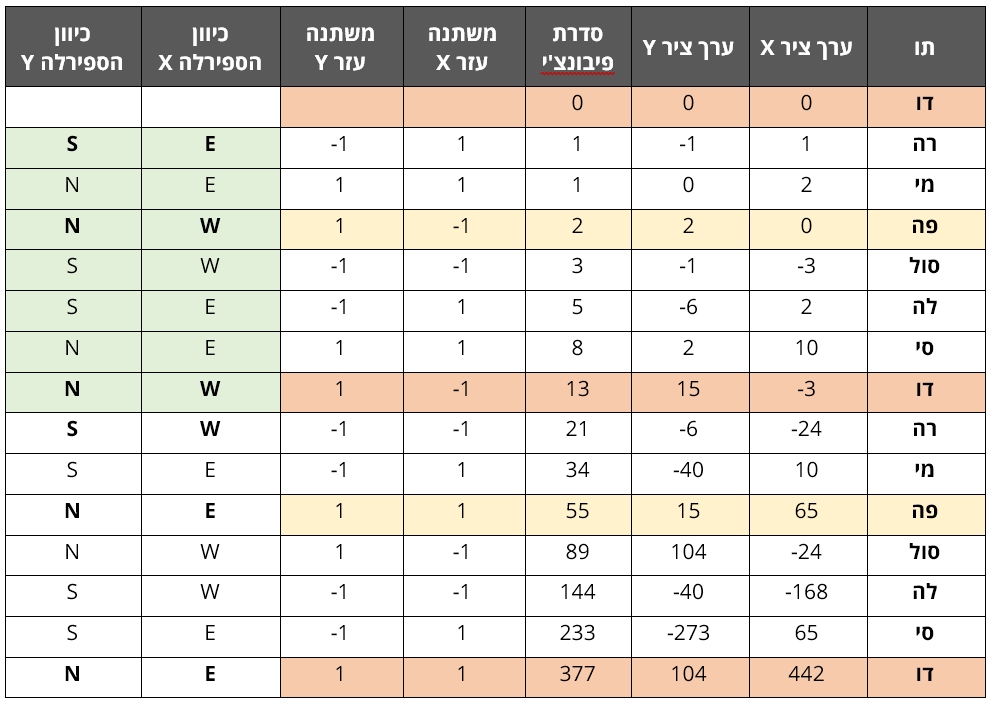
התרגום של סדרת פיבונצ'י לערכי X ו-Y שייצרו ספירלה נעשה באמצעות משתני עזר לכל אחד מהצירים. כל משתנה עזר מורכב מצמדים של 1 ו-1 ולאחר מכן (1-) ו- (1-) וחוזר חלילה. משתנה העזר ל-X מתחיל בערך 1 בעוד שמשתנה העזר ל-Y מתחיל בערך (1-). כל ערך של X ו-Y שווה לערך הקודם ועוד המכפלה של משתנה העזר באיבר פיבונצ'י המתאים.
לדוגמה:
ערך ה-X שמקביל לתו פה באוקטבה הראשונה הוא 0. הוא מתקבל באמצעות הערך הקודם (של התו מי) שהוא 2 ועוד משתנה העזר (1-) כפול איבר פיבונצ'י המתאים (2).
במקביל ערך ה-Y שמקביל לתו פה באוקטבה הראשונה הוא 2, והוא מתקבל באמצעות הערך הקודם שהוא 0 ועוד משתנה העזר (1) כפול איבר פיבונצ'י המתאים (2).
ערך ה-X שמקביל לתו פה באוקטבה השנייה הוא 65. הוא מתקבל באמצעות הערך הקודם (של התו מי) שהוא 10 ועוד משתנה העזר (1) כפול איבר פיבונצ'י המתאים (55).
במקביל ערך ה-Y שמקביל לתו פה באוקטבה השנייה הוא 15, והוא מתקבל באמצעות הערך הקודם שהוא 40- ועוד משתנה העזר (1) כפול איבר פיבונצ'י המתאים (55).
באופן זה ניתן ליצור ערכי X ו-Y שהשרטוט שלהם על פני מערכת צירים ייתן לנו את ספירלת פיבונצ'י. בתרשים שלהלן מוצג שרטוט של האוקטבה הראשונה.
אוקטבה ראשונה
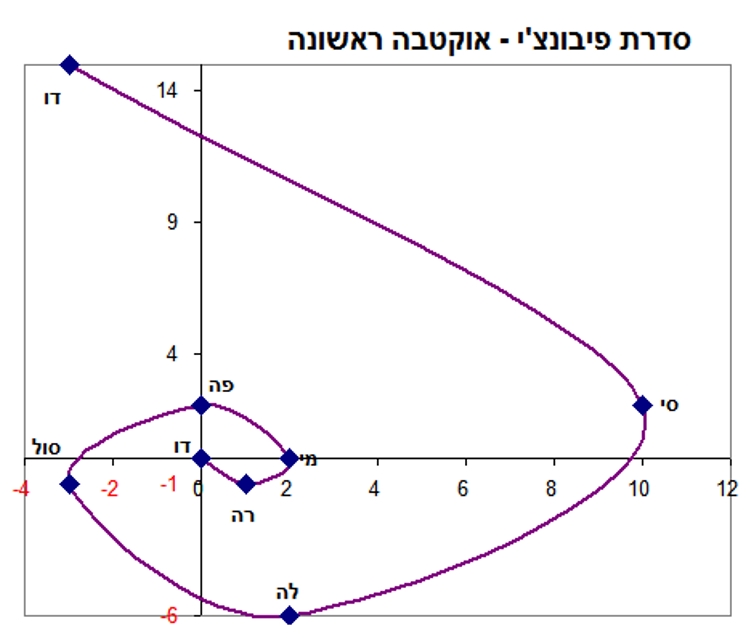
ליד כל אחת מהנקודות מסומן גם התו המתאים לה. הספירלה בתרשים זה זהה בעקרון לספירלה הסכמטית שהוצגה קודם, שנוצרה על ידי החיצים שהועברו דרך אלכסוני הריבועים של חתך הזהב. כיוון הספירלה במקטעים השונים שלה מוצג בטבלה הבאה והוא זהה לכיוונים שראינו בתרשים הקודם. הספירלה מתחילה מהנקודה 0,0 לכיוון דרום מזרח.

כמו בדוגמה הקודמת הספירלה הופכת את כיוונה ביחס לכיוון ההתחלתי פעמיים: בין התווים מי לפה ובין התווים סי לדו.
התרשים הבא מציג את ספירלה שנוצרה באוקטבה השנייה. ספירלה זו מתחילה באיבר 13 בסדרת פיבונצ'י ומסתיימת באיבר 377 (ראו טבלה מתחת לתרשים).
אוקטבה שנייה
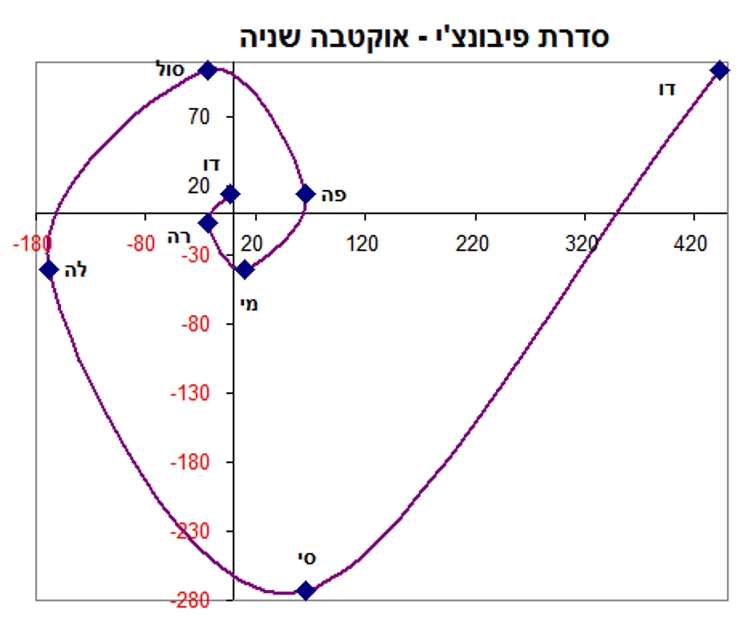
הספירלה של האוקטבה השנייה מתחילה לכיוון דרום־מערב, וגם היא הופכת את כיוונה ביחס לכיוון ההתחלתי פעמיים: בין התווים מי לפה ובין התווים סי לדו. ניתן לראות שהפיכת הכיוון ביחס לכיוון המקורי על פי חוק האוקטבה איננה תלויה בכיוון ההתחלתי של הספירלה, אלא היא תכונה של ספירלת פיבונצ'י.
אפשר לראות בספירלת פיבונצ'י ביטוי גרפי לחוק האוקטבה. חוק האוקטבה אמנם מבטא מחזוריות, מכיוון שבכל אוקטבה התווים חוזרים על עצמם. אולם זו איננה מחזוריות מעגלית, מכיוון שלכל תו יש תדר גבוה יותר מזה שלפניו, עד שמתחילה אוקטבה חדשה שבה התדר מוכפל. הספירלה מבטאת באופן גרפי את התכונות האלה. מצד אחד יש בה מחזוריות בגלל התנועה המעגלית, אולם כל מעגל גדול יותר מזה שלפניו.
העניין בספירלות פיבונצ'י איננו מתמטי בלבד, מכיוון שספירלות כאלה נפוצות מאוד בטבע.
להלן נציג מספר דוגמאות:
בעולם החי ניתן לראות ספירלות פיבונצ'י בתבניות ההתפתחות של שבלולים וקונכיות.

ניתן לראות כיצד הקונכייה מתפתחת מבפנים החוצה בצורת ספירלה.
בעולם הצומח התפתחות של עלים בצמחים היא לעתים קרובות מאוד בצורת ספירלה, כפי שממחישות שתי התמונות הבאות.

העלים צומחים מבפנים החוצה ויוצרים ספירלה שהולכת וגדלה. תבניות דומות ניתן למצוא גם בהתפתחות של זרעים בתוך פרחים וכן בהתפתחות של עלי כותרת. באופן כמעט קבוע אנו רואים צמיחה מבפנים החוצה בצורה של ספירלה. מדענים טוענים שהצורה הספירלית מתפתחת בטבע מכיוון שהיא מספקת את היעילות האנרגטית הגבוהה ביותר.
סופות באטמוספירה גם הן מתפתחות בצורה של ספירלת פיבונצ'י, כמי שממחיש צילום האוויר של ההוריקן קטרינה.

גם גלקסיית שביל החלב, שבה נמצאת מערכת השמש שלנו, בנויה כספירלת פיבונצ'י.

יואב ויזל – פרופסור לבוטניקה באוניברסיטת תל אביב – מתייחס לחוקיות שבאה לידי ביטוי בצורת הספירלה במאמר שהתפרסם במגזין "מחשבות":
"דוגמה נוספת לאחידות ולקביעות של צורות היסוד של החיים היא צורת הסליל.
סליליות בצמחים מתבטאת בגדילי הדנ״א, בהשקעת אגדי מולקולות התאית (פיברילות) בדופן התא, בסידור תאי הגבעול, בסידור העלים לאורך הציר, בסידור הפרחים בתפרחת, באתרי יציאת השורשים הצדדיים בשורשים ועוד. סליליות פירושה חוקיות. לפיכך, הכרת מקומם של שלושת הפרחים הראשונים בתפרחת של חמנית והכרת החוקיות של הסליל בצמח זה מאפשרת חיזוי מדויק של מקומם של שאר הפרחים".
לסיכום ההתפתחות של צורות רבות בטבע בתבנית של ספירלה מבטאת חוקיות שניתן לתאר אותה בצורה גיאומטרית באמצעות "יחס הזהב", ובצורה מתמטית באמצעות סדרת פיבונצ'י. המבנה הייחודי של צורת הספירלה מבטא את חוק האוקטבה שבא לידי ביטוי בנקודות המפנה שלה.
לקריאת המאמר המלא "אבולוציה, תודעה וחוק האוקטבה" מאת אלי מלכי.
***
הסרטון nature by numbers מאת כריסטובל וילה ממחיש איך דברים שונים בטבע מבוססים על סדרת פיבונצ'י וחתך הזהב:






תגובות גולשים
כמה מילים לאלי מלכי.
אי אפשר שלא להתרשם מהביטויים הגרפיים של חוק השבע כפי שהם מוצגים בכתבה. אך בעודנו מתפעלים מהקשירות המתמטית של החוק, יש מקום לזכור שהם היבטים השייכים לעולם המושגים הארצי ואילו חוק השבע, מתאר גם ובעיקר מציאות קוסמית שלא ניתן לבטא אותה במושגים ארציים.
הבנת מה של חוק השבע (וחוק השלושה המשלים אותו) דורשת חשיבה מסוג אחר, משהו קרוב להתנסות או ראייה ישירה לעומק הדברים. נכון, לא ניתן לתאר זאת בכתבה מילולית בעיתון, אך ניתן לפתח כלים קוגניטיביים שפותחים שערים חדשים "לעולם האמתי" כפי שגורדייף מכנה זאת.